알고리즘 복잡도 표현 방법

1. 알고리즘 복잡도 계산이 필요한 이유

2. 알고리즘 복잡도 계산 항목

알고리즘 복잡도계산 항목

생각해보기

프로그래밍에서 시간 복잡도에 가장 영향을 많이 미치는 요소는 반복문

알고리즘 성능 표기법

3. 대문자 O 표기법

4. 실제 알고리즘을 예로 각 알고리즘의 시간 복잡도와 빅 오 표기법 알아보기

연습 1 : 1부터 n까지의 합을 구하는 알고리즘 작성해보기

알고리즘 1 : 1부터 n까지의 합을 구하는 알고리즘 1

시간 복잡도 구하기

알고리즘 2 : 1부터 n까지의 합을 구하는 알고리즘 2

시간 복잡도 구하기

어느 알고리즘이 성능이 좋은가요

요약

 

1. 알고리즘 복잡도 계산이 필요한 이유

• 하나의 문제를 푸는 알고리즘은 다양할 수 있음

 

• 정수의 절대값 구하기1,-1 - >> 1
  • 방법1 : 정수값을 제곱한 값에 다시 루트를 씌우기
  • 방법2 : 정수가 음수인지 확인해서, 음수일 때만, -1을 곱하기
  다양한 알고리즘 중 어느 알고리즘이 더 좋은지를 분석하기 위해, 복잡도를 정의하고 계산함
•  

2. 알고리즘 복잡도 계산 항목

1. 시간 복잡도 : 알고리즘 실행 속도

2. 공간 복잡도 : 알고리즘이 사용하는 메모리 사이즈

가장 중요한 시간 복잡도를 꼭 이해하고 계산할 수 있어야 함

 

알고리즘 복잡도계산 항목

반복문이 지배.

 

생각해보기

• 자동차로 서울에서 부산을 가기 위해 다음과 같이 항목을 나누었을 때 가장 총 시간에 영향을 많이 미칠 것 같은 요소는?자동차로 서울에서 부산가기
  1. 자동차 문열기
  2. 자동차 문닫기
  3. 자동차 운전석 등받이 조정하기
  4. 자동차 시동걸기
  5. 자동차로 서울에서 부산가기
  6. 자동차 시동끄기
  7. 자동차 문열기
  8. 자동차 문닫기

프로그래밍에서 시간 복잡도에 가장 영향을 많이 미치는 요소는 반복문

• 입력의 크기가 커지면 커질수록 반복문이 알고리즘 수행 시간을 지배함

 

알고리즘 성능 표기법

• Big O(빅 오) 표기법 : O(N)
  • 알고리즘 최악의 실행 시간을 표기
  • 가장 많이/일반적으로 사용함
  • 아무리 최악의 상황이라도, 이정도의 성능은 보장한다는 의미이기 때문

• 오메가 표기법 : Ω(N)
  • 오메가 표기법은 알고리즘 최상의 실행 시간을 표기

• 세타 표기법 : θ(N)
  • 세타 표기법은 알고리즘 평균 실행시간을 표기

시간복잡도 계산은 반복문이 핵심 요소임을 인지하고, 계산 표기는 최상, 평균, 최악 중, 최악의 시간인 Big-O 표기법을 중심으로 익히면 됨.

3. 대문자 O 표기법

• 빅 오 표기법, Big-O 표기법 이라고도 부름

• O(입력)
  • 입력 n에 따라 결정되는 시간 복잡도 함수
  • $O(1),O(logn),O(n),$$O$($nlogn$),$O(n^2),O(2^n),O(n!)$등으로 표기함
  • 입력 n의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있음
    • $O(1)<O(logn)<O(n)<O(nlogn)<O{(}^2)<O(2^n)<O(n!)$
    • 참고 : logn의 베이스는 2 - log2n
  • 단순하게 입력 n에 따라 몇번 실행이 되는지를 계산하면 됨
    • 표현식에 가장 큰 영향을 미치는 n의 단위로 표기함.
    • n이 1이든 100이든, 1000이든 100000이든 실행을
      • 무조건 2회(상수회) 실행한다 : O(1)

        if n > 10: 	print(n)

      • n에 따라, n번, n + 10번 또는 3n + 10 번등 실행한다. : O(n)

        variable = 1 for num in range(3): 	for index in range(n): 		print(index)

      • n에 따라$n^2$번,$n^2$ + 100번 또는$100n^2-100$ 번등 실행한다. :$O(n^2)$상상순

        variable = 1 for i in range(300): 	for num in range(n): 		for index in range(n): 			print(index)

    

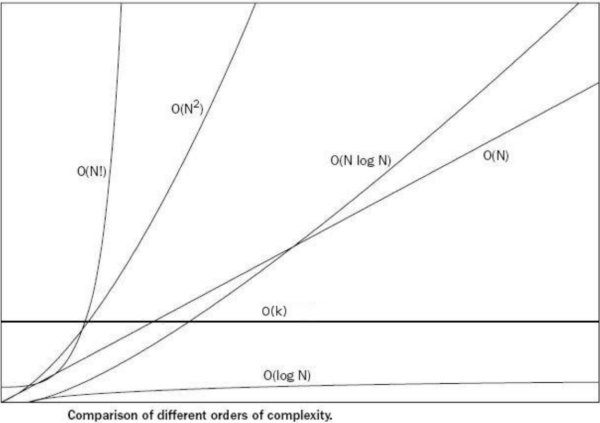
    • 빅 오 입력값 표기 방법
      • 만약 시간 복잡도 함수가$2n^2+3n$이라면 (최고차항 외 다른 숫자는 제거)
        • 가장 높은 차수는$2n^2$
        • 상수는 실제 큰 영향이 없음
        • 결국 빅 오 표기법으로는$O(n^2)$ (서울부터 부산까지 가는 자동 차의 예를 상기)

4. 실제 알고리즘을 예로 각 알고리즘의 시간 복잡도와 빅 오 표기법 알아보기

연습 1 : 1부터 n까지의 합을 구하는 알고리즘 작성해보기

알고리즘 1 : 1부터 n까지의 합을 구하는 알고리즘 1

• 합을 기록할 변수를 만들고 0을 저장

• n을 1부터 1씩 증가하면서 반복

• 반복문 안에서 합을 기록할 변수에 1씩 증가된 값을 더함

• 반복이 끝나면 합을 출력

def sum_all(n): # n의 갯수에 따라서 "반복문"이 실행. 따라서 n번 만큼 반복문 실행 	total = 0 for num in range(1,n+1): 	total += num return total -------------------------------- sum_all(100) -------------------------------- 5050

시간 복잡도 구하기

1부터 n까지의 합을 구하는 알고리즘 1

• 입력 n에 따라 덧셈을 n번 해야 함(반복문)

• 시간 복잡도 : n, 빅 오 표기법으로는 O(n)

알고리즘 2 : 1부터 n까지의 합을 구하는 알고리즘 2

• $\frac{n(n+1)}{2}$

def sum_all(n): # 어떤 수가 들어오던 간에 반복문이 없다.     return int(n * (n + 1) / 2) ------------------------------ sum_all(100) ------------------------------ 5050

시간 복잡도 구하기

• 1부터 n까지의 합을 구하는 알고리즘 2
  • 입력 n이 어떻든 간에,곱셈,덧셈,나눗셈 하면 됨(반복문이 없음)
  • 시간 복잡도 : 1, 빅 오 표기법으로는 O(1)

 

어느 알고리즘이 성능이 좋은가요

• 알고리즘 1 vs 알고리즘 2
  • O(n) vs O(1)

이와 같이 동일한 문제를 푸는 알고리즘은 다양할 수 있음 어느 알고리즘이 보다 좋은지를 객관적으로 비교하기 위해 빅 오 표기법 등의 시간복잡도 계산법을 사용함.

요약

시간 복잡도 계산을 위해 반복문은 알고리즘 복잡도에 매우 중요한 요소로 간주됩니다. 그래서 이를 이해하고 계산하기 위해 Big-O 표기법을 중심으로 많은 시간과 노력을 기울이는 것이 필수적입니다. 또한 이러한 복잡도를 계산하는 것에 대한 방법론과 이해가 필요합니다. 실제로 이러한 복잡도는 코드의 성능과 메모리 사용량에 큰 영향을 미치기 때문에 반드시 고려해야 합니다.

Uploaded by

N2T